Polinômios

Um polinômio se parece com isso:

exemplo de um polinômio este tem 3 termos

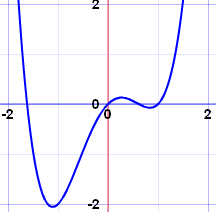
Polinômios com uma variável fazem belas curvas suaves:

Um polinômio pode ter:

constantes (como3,−20, ou½)

variáveis ​​(como x e y )

expoentes (como o 2 em y2), mas apenas0, 1, 2, 3, ... etc, são permitidos

e podem ser combinados usando adição, subtração, multiplicação e divisão ...

Um polinômio pode ter constantes, variáveis ​​e expoentes,
mas nunca divisão por uma variável.

Também podem ter um ou mais termos, mas não um infinito número de termos.

Polinômio ou não?

São polinômios :

3x
x − 2
−6a ² − (79) x
3xyz + 3xy ² z − 0,1xz − 200y + 0,5
512v ⁵ + 99w ⁵
5

(Sim, "5" é um polinômio, um termo é permitido e pode ser apenas uma constante!)

 

não são polinômios

• 3xy ^-2 não é, porque o expoente é "-2" (expoentes só podem ser 0,1,2,...)
• 2/(x+2) não é, porque a divisão por uma variável não é permitida
• 1/x também não é
• √x não é, porque o expoente é "½" (veja expoentes fracionários )

 

Mas estes são permitidos:

• x/2 é permitido , porque você pode dividir por uma constante
• também 3x/8 pelo mesmo motivo
• √2 é permitido, pois é uma constante (= 1,4142...etc)

Monômio, Binômio, Trinômio

Existem nomes especiais para polinômios com 1, 2 ou 3 termos:

Há também quadrinomial (4 termos) e quintinomial (5 termos),
mas esses nomes não são usados ​​com frequência.

Variáveis

Polinômios não podem ter nenhuma variável

Exemplo: 21 é um polinômio. Tem apenas um termo, que é uma constante.

Ou uma variável

Exemplo: x ⁴ − 2x ² + x   tem três termos, mas apenas uma variável (x)

Ou duas ou mais variáveis

Exemplo: xy ⁴ − 5x ² z   tem dois termos e três variáveis ​​(x, y e z)

O que há de especial nos polinômios?

Devido à definição estrita, os polinômios são fáceis de trabalhar .

Por exemplo, sabemos que:

• Se você adicionar polinômios, obterá um polinômio
• Se você multiplicar polinômios, obterá um polinômio

Então você pode fazer muitas adições e multiplicações e ainda ter um polinômio como resultado.

Além disso, os polinômios de uma variável são fáceis de representar graficamente, pois possuem linhas suaves e contínuas.

Exemplo: x ⁴ −2x ² +x

Representação gráfica da função polinomial.

Você também pode dividir polinômios (mas o resultado pode não ser um polinômio).

Grau

O grau de um polinômio com apenas uma variável é o maior expoente dessa variável.

Exemplo:

4x 3 − x + 2

O Grau é 3 (o maior expoente de x )

Forma padrão

A Forma padrão para escrever um polinômio é colocar os termos com o maior grau primeiro.

Exemplo: coloque isso na forma padrão: 3 x ² − 7 + 4 x ³ + x ⁶

O grau mais alto é 6, então esse vai primeiro, depois 3, 2 e depois a constante por último:

x ⁶ + 4 x ³ + 3 x ² − 7

Você não precisa usar a forma padrão, mas ajuda.