Trabalhando com expoentes e logaritmos

O que é um Expoente?

O expoente de um número diz quantas vezes usar o número em uma multiplicação. Neste exemplo: 2 3 = 2 × 2 × 2 = 8 (2 é usado 3 vezes em uma multiplicação para obter 8)

O que é um logaritmo?

Um Logaritmo vai para o outro lado.

Ele faz a pergunta "qual expoente produziu isso?":

E responde assim:

Nesse exemplo:

• O expoente pega 2 e 3 e dá 8 (2, usado 3 vezes em uma multiplicação, dá 8)
• O logaritmo pega 2 e 8 e dá 3 (2 dá 8 quando usado 3 vezes em uma multiplicação)

Um logaritmo diz quanto de um número deve ser multiplicado para obter outro número

Portanto, um logaritmo realmente nos dá o expoente como sua resposta :

Trabalhando juntos

Expoentes e logaritmos juntos funcionam bem porque eles "desfazem" um ao outro (desde que a base "a" seja a mesma):

Eles são "Funções inversas"

 

Fazendo um, depois o outro, nos leva de volta para onde começamos:

Fazendo a^x então log _a nos dá de volta x :log _a (a ^x ) = x

Fazendo log _a então a ^x nos devolve x :um ^log _a (x) = x

 

É uma pena que eles sejam escritos de forma tão diferente ... isso faz as coisas parecerem estranhas. Portanto, pode ajudar pensar em a ^x como "para cima" e registrar _a (x) como "para baixo": 

De qualquer forma, o importante é que:

A Função Logarítmica é "desfeita" pela Função Exponencial.

(e vice versa)

Como neste exemplo:

Exemplo, quanto é x no log ₃ (x) = 5

Queremos "desfazer" o log ₃ para podermos obter "x ="

Começar com:log ₃ (x) = 5

Use a função exponencial em ambos os lados:3 ^{log ₃ (x)} = 3 ⁵

E sabemos que 3 ^{log ₃ (x)} = x , então:x = 3 ⁵

Resposta:x = 243

E também:

Exemplo: Calcular y em y = log ₄ (14)

Começar com:y = log ₄ (14)

Use a função exponencial em ambos os lados:4 ^y = 4 ^{log ₄ (14)}

Simplificar:4 ^y =14

Agora um truque simples:14= 4 ^-1

Então:4 ^y = 4 ^-1

E assim:y = −1

Propriedades dos logaritmos

Uma das coisas poderosas sobre logaritmos é que eles podem transformar multiplicação em adição .

log_a (m × n) = log_a m + log_a n

"o logaritmo da multiplicação é a soma dos logs"

Por que isso é verdade?

Usando essa propriedade e a Leis dos Expoentes obtemos estas propriedades úteis:

loga (m × n) = loga m + loga n	o log da multiplicação é a soma dos logs
loga (m/n) = loga m − loga n	o log da divisão é a diferença dos logs
loga (1/n) = −log a n	isso segue a regra de "divisão" anterior, porque log a (1) = 0
loga (mr ) = r ( loga m )	o log de m com um expoente r é r vezes o log de m

Lembre-se: a base "a" é sempre a mesma!

História: Os logaritmos eram muito úteis antes das calculadoras serem inventadas... por exemplo, em vez de multiplicar dois números grandes, usando logaritmos podemos transformá-lo em adição (muito mais fácil!)

E havia livros cheios de tabelas de logaritmos para ajudar.

Vamos nos divertir usando as propriedades:

Exemplo: Simplifique log _a ( (x ² +1) ⁴ √x )

Começar com:log _a ((x ² +1) ⁴ √x)

Use log _a (mn) = log _a m + log _a n :log _a ( (x ² +1) ⁴ ) + log _a ( √x )

Use log _a (m ^r ) = r ( log _a m ) :4 log _a (x ² +1) + log _a ( √x )

Também √x = x ^½ :4 log _a (x ² +1) + log _a ( x ^½ )

Use log _a (m ^r ) = r ( log _a m ) novamente:4 log _a (x ² +1) + ½ log _a (x)

Isso é o máximo que podemos simplificar ... não podemos fazer nada com log _a (x ² +1)

 

Resposta: 4 log _a (x ² +1) + ½ log _a (x)

Nota: não há regra para lidar com log _a (m+n) ou log _a (m−n)

 Também podemos aplicar as regras do logaritmo "ao contrário" para combinar logaritmos:

Exemplo: Transforme isso em um logaritmo: log _a (5) + log _a (x) − log _a (2)

Começar com:log _a (5) + log _a (x) − log _a (2)

Use log _a (mn) = log _a m + log _a n :log _a (5x) − log _a (2)

Use log _a (m/n) = log _a m − log _a n :log _a (5x/2)

 

Resposta: log _a (5x/2)

O logaritmo natural e as funções exponenciais naturais

Quando a base é Número de Euler e = 2,718281828459... obtemos:

• O Logaritmo Natural log _e (x) que é mais comumente escrito ln(x)
• A Função Exponencial Natural e ^x

E a mesma ideia de que um pode "desfazer" o outro ainda é verdadeira:

ln(e ^x ) = x

e ^{(ln x)} = x

E aqui estão seus gráficos:

Logaritmo natural		Função Exponencial Natural
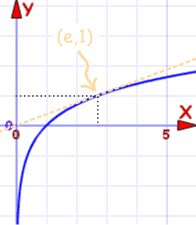Gráfico de f(x) = ln(x)		Gráfico de f(x) = e x
Passa por (1,0) e (e,1)		Passa por (0,1) e (1,e)

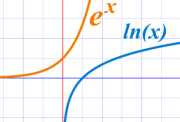
Eles são a mesma curva com o eixo x e o eixo y invertidos .

O que é outra coisa que nos mostra que são funções inversas.

Em uma calculadora, o logaritmo natural é o botão "ln".

Sempre tente usar Logaritmos Naturais e a Função Exponencial Natural sempre que possível.

O logaritmo comum

Quando a base é 10 temos:

O logaritmo comum log ₁₀ (x) , que às vezes é escrito como log(x)

Os engenheiros adoram usá-lo, mas não é muito usado em matemática.

Em uma calculadora, o logaritmo comum é o botão "log". É útil porque nos diz quão "grande" é o número em decimal (quantas vezes precisamos usar 10 em uma multiplicação).

Exemplo: Calcular log ₁₀ 100

Bem, 10 × 10 = 100, então quando 10 é usado 2 vezes em uma multiplicação, obtemos 100:

log ₁₀ 100 = 2

Da mesma forma, log ₁₀ 1,000 = 3, log ₁₀ 10,000 = 4 e assim por diante.

Exemplo: Calcular log ₁₀ 369

OK, melhor usar o botão "log" da minha calculadora:

log ₁₀ 369 = 2.567...

Mudando a base

E se quisermos mudar a base de um logaritmo?

Fácil! Basta usar esta fórmula:

"x sobe, a desce"

1log _b afunciona como um "fator de conversão" de uma base para qualquer outra base.

Outra propriedade útil é:

log _a x = 1 / log _x a

Veja como "x" e "a" trocam de posição?

Exemplo: Calcular 1 / log ₈ 2

1 / log ₈ 2 = log ₂ 8

E 2 × 2 × 2 = 8, então quando 2 é usado 3 vezes em uma multiplicação, obtemos 8:

1 / log ₈ 2 = log ₂ 8 = 3

 

E usamos o logaritmo natural com tanta frequência que vale a pena lembrar disso:

log _a x = ln x / ln a

 

Exemplo: Calcular log ₄ 22

Minha calculadora não tem botão " log 4 "... ... mas tem um botão " ln ", então podemos usar isso:

log ₄ 22 =ln 22 / ln 4

=3,09... / 1,39...

=2,23 (com 2 casas decimais)

 

O que essa resposta significa? Isso significa que 4 com um expoente de 2,23 é igual a 22. Portanto, podemos verificar essa resposta:

Verifique: 4 ^2,23 = 22,01 (perto o suficiente!)

Aqui está outro exemplo:

Exemplo: Calcular log ₅ 125

Podemos usar a função "ln" na calculadora:

registro ₅ 125 =ln 125 / ln 5

=4,83... / 1,61...

=3,00 (com 2 casas decimais)

São exatamente 3? Não devemos confiar em uma calculadora, pois pode haver erros de arredondamento, mas neste caso podemos verificar que 5 ³ = 5 × 5 × 5 = 125 exatamente , então:

Resposta: 3

Uso no mundo real

Aqui estão alguns usos para logaritmos no mundo real:

Terremotos

A magnitude de um terremoto é uma escala logarítmica.

A famosa "Escala Richter" usa esta fórmula:

M = log ₁₀ A + B

Onde A é a amplitude (em mm) medida pelo sismógrafo
e B é um fator de correção de distância

Hoje em dia existem fórmulas mais complicadas, mas ainda usam uma escala logarítmica.

Som

O volume é medido em decibéis (dB para abreviar):

 dB = 10 log ₁₀ (p × 10 ¹² )

onde p é a pressão sonora.

Ácido ou Alcalino

A acidez (ou alcalinidade) é medida em pH:

pH = −log ₁₀ [H ⁺ ]

onde H ⁺ é a concentração molar de íons de hidrogênio dissolvidos.
Nota: em química [ ] significa concentração molar (moles por litro).

Mais exemplos

Exemplo: Resolva 2 log ₈ x = log ₈ 16

Começar com:2 log ₈ x = log ₈ 16

Traga o "2" para o log:log ₈ x ² = log ₈ 16

Remova os logs (eles são a mesma base):x ² = 16

Resolver:x = −4 ou +4

Mas, não podemos ter um logaritmo de um número negativo!

Portanto, o caso −4 não será desconsiderado.

Resposta: 4

Verifique: use uma calculadora para ver se esta é a resposta certa... tente também o caso "-4".

Exemplo: Resolva e ^− w = e ^2w+6

Começar com:e ^-w = e ^2w+6

Aplique ln em ambos os lados:ln(e ^-w ) = ln(e2w ⁺⁶ )

E ln(e ^w )=w :−w = 2w+6

Simplificar:−3w = 6

Resolver:w = 6/−3 = −2

Resposta: w = − 2

Verifique: e ^-(−2) = e ² e e ^2(−2)+6 = e ²

 

Por que log(m × n) = log(m) + log(n) ?

Para ver por que ^, usaremos log ^_a (x) = x e log _a (a ^x ) = x assim:

Parece que complicamos as coisas ao transformar em log ^a ₍ x) , mas depois podemos adicioná-los, transformamos novamente e temos uma solução!

É uma daquelas transformações que fazemos em matemática.