Simplificando Raízes Quadradas
Para simplificar uma raiz quadrada: torne o número dentro da raiz quadrada o menor possível (mas ainda um número inteiro ):
Exemplo: √12 é mais simples como 2√3
Pegue sua calculadora e confira se quiser: os dois são o mesmo valor!
Aqui está a regra: quando a e b não são negativos

E aqui está como usá-lo:
Exemplo: simplificar √12
12 é 4 vezes 3:
√12 = √(4 . 3)
Use a regra:
√(4 . 3) = √4 . √3
E a raiz quadrada de 4 é 2:
√4 . √3 = 2√3
Então √12 é mais simples como 2√3
Outro exemplo:
Exemplo: simplificar √8
√8 = √(4.2) = √4 . √2 = 2√2
(Porque a raiz quadrada de 4 é 2)
E outro:
Exemplo: simplificar √18
√18 = √(9 . 2) = √9 . √2 = 3√2
Muitas vezes ajuda a fatorar os números (em números primos é melhor):
Exemplo: simplificar √6 . √15
Primeiro podemos combinar os dois números:
√6 . √15 = √(6 . 15)
Então nós os fatoramos:
√(6 × 15) = √(2 × 3 × 3 × 5)
Então vemos dois 3 e decidimos "retirá-los":
√(2 . 3 . 3 . 5) = √(3 . 3) . √(2 . 5) = 3√10
Frações
Existe uma regra semelhante para frações:
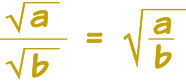
Exemplo: simplificar √30 / √10
Primeiro podemos combinar os dois números:
√30 / √10 = √(30 / 10)
Então simplifique:
√(30/10) = √3
Alguns exemplos mais difíceis
Exemplo: simplificar 2√12 + 9√3
Primeiro simplifique 2√12:
2√12 = 2 . 2√3 = 4√3
Agora ambos os termos têm √3, podemos adicioná-los:
4√3 + 9√3 = (4+9)√3 = 13√3
![]()
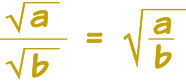



Nenhum comentário:
Postar um comentário