Proporções

A proporção diz que dois índices(ou frações) são iguais.

Exemplo:

Dizemos que 1 em 3 é igual a 2 em 6

As proporções são as mesmas.

Exemplo:

O comprimento e o peso de uma corda são proporcionais.

Quando 20m de corda pesam 1kg , então:

• 40m dessa corda pesa 2kg
• 200m dessa corda pesam 10kg
• etc.

Então:

201=402

Tamanhos

Quando as formas são "proporcionais", seus tamanhos relativos são os mesmos.

Aqui vemos que as proporções entre o comprimento da cabeça e o comprimento do corpo são as mesmas em ambos os desenhos. Portanto, são proporcionais . Fazer a cabeça muito longa ou curta ficaria ruim!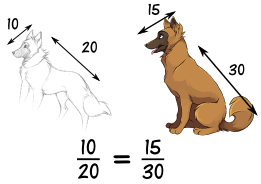

Exemplo: tamanhos de papel padrão internacionais (como A3, A4, A5, etc) têm as mesmas proporções:

Portanto, qualquer arte ou documento pode ser redimensionado para caber em qualquer folha.

Trabalhando com Proporções

AGORA, como usamos isso?

Exemplo: você quer desenhar a cabeça do cachorro ... qual a medida?

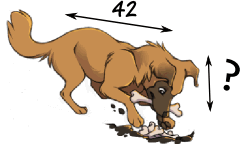
Vamos definir a proporção acima como 10/20:

?42=1020

Agora resolvemos usando um método especial:

Multiplique os extremos

E obtemos isto:

? x 20= 42 × 10

? = (42 × 10) / 20

= 420 / 20

= 21

Então nós devemos desenhar a cabeça 21 de comprimento.

Usando proporções para resolver porcentagens

Uma porcentagem é na verdade uma proporção! Dizer "25%" é na verdade dizer "25 por 100":

25% =25100

Podemos usar proporções para resolver questões envolvendo porcentagens.

O truque é colocar o que sabemos neste formulário: 

Exemplo: quanto é 25% de 160?

A porcentagem é 25, o todo é 160 e queremos encontrar a "parte":

parte
160=25100

Multiplique os extremos:

Parte x 100= 160 × 25

Parte = (160 × 25) / 100

= 4000 / 100
= 40

Resposta: 25% de 160 é 40.

 

Nota: também poderíamos ter resolvido isso fazendo a divisão primeiro, assim:

Parte = 160 × (25/100)
= 160 × 0,25
= 40

Qualquer método funciona bem.

Também podemos encontrar uma porcentagem:

Exemplo: R$ 12 é quantos por cento de R$ 80?

Preencha o que sabemos:

 12 80=Por cento100

Multiplique pelos cantos conhecidos e divida pelo terceiro número. Desta vez, os cantos conhecidos são superior esquerdo e inferior direito:

Porcentagem = (12 × 100) / 80

= 1200 / 80
= 15%

Resposta: R$ 12 é 15% de R$ 80

Ou encontre o Todo:

Exemplo: o preço de venda de um telefone era R$ 150, o que representava apenas 80% do preço normal. Qual era o preço normal?

Preencha o que sabemos:

R$ 150Todo=80100

Multiplique pelos cantos conhecidos e divida pelo terceiro número:

Inteiro = (R$ 150 × 100) / 80

= 15.000 / 80
= 187,50

Resposta: o preço normal do telefone era R$187,50

Usando proporções para resolver triângulos

Podemos usar proporções para resolver triângulos semelhantes.

Exemplo: Qual é a altura da Árvore?

Jonny tentou usar uma escada, fita métrica, cordas e várias outras coisas, mas ainda não conseguia descobrir a altura da árvore.

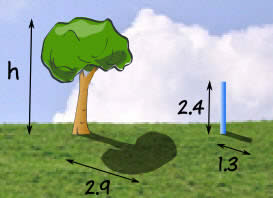
Então Jonny tem uma ideia inteligente... triângulos semelhantes!

Jonny mede uma vara e sua sombra (em metros), e também a sombra da árvore, e é isso que ele obtém:

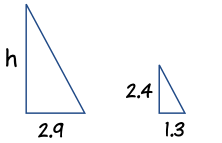
Agora Jonny faz um esboço dos triângulos e anota a relação "Altura para Comprimento" para ambos os triângulos:

Altura:Comprimento da Sombra:     h2,9m = 2,4m1,3m

Multiplique pelos cantos conhecidos e divida pelo terceiro número:

h = (2,9 × 2,4) / 1,3
= 6,96 / 1,3
= 5,4 m 

Resposta: a árvore tem 5,4 m de altura.

E ele nem precisou de escada!

A "Altura" poderia estar no denominador, desde que estivesse na parte inferior para ambas as proporções, assim:

Vamos tentar a proporção de "Comprimento da Sombra para Altura":

Comprimento da Sombra:Altura:     2,9mh = 1,3m2,4m

Multiplique pelos cantos conhecidos e divida pelo terceiro número:

h = (2,9 × 2,4) / 1,3
= 6,96 / 1,3
= 5,4 m (para o 0,1 mais próximo)

É o mesmo cálculo anterior.

Um exemplo "concreto"

As razões podem ter mais de dois números !

Por exemplo, o concreto é feito misturando cimento, areia, pedras e água.

Uma mistura típica de cimento, areia e pedras é escrita como uma proporção, como 1:2:6 .

Podemos multiplicar todos os valores pela mesma quantidade e ainda ter a mesma proporção.

10:20:60 é igual a 1:2:6

Então, quando usamos 10 baldes de cimento, devemos usar 20 de areia e 60 de pedras.

Exemplo: você acabou de colocar 12 baldes de pedras em um misturador, quanto cimento e quanto areia você deve adicionar para fazer uma mistura 1:2:6 ?

Vamos colocar em uma tabela para ficar mais claro:

	Cimento	Areia	pedras
Razão Necessária:	1	2	6
Você tem:			12

Você tem 12 baldes de pedras, mas a proporção diz 6.

Tudo bem, você simplesmente tem o dobro de pedras do número na proporção ... então você precisa do dobro de tudo para manter a proporção.

Aqui está a solução:

	Cimento	Areia	pedras
Razão Necessária:	1	2	6
Você tem:	2	4	12

E a proporção 2:4:12 é a mesma que 1:2:6 (porque eles mostram os mesmos tamanhos relativos )

Então a resposta é: adicione 2 baldes de Cimento e 4 baldes de Areia. (Você também vai precisar de água e muita agitação....)

Por que eles são a mesma proporção? Bem, a proporção 1:2:6 diz ter :

• duas vezes mais areia do que cimento ( 1 : 2 :6)
• 6 vezes mais pedras do que cimento ( 1 :2: 6 )

Em nosso mix temos:

• duas vezes mais areia do que cimento ( 2 : 4 :12)
• 6 vezes mais pedras do que cimento ( 2 :4: 12 )

Então deve estar certo!

Essa é a coisa boa sobre as proporções. Você pode aumentar ou diminuir os valores e, desde que os tamanhos relativos sejam os mesmos, a proporção é a mesma.