Produtos notáveis

Veja o que acontece quando multiplicamos alguns binômios...

binômio

Um binômio é um polinômio com dois termos

exemplo de binômio

produtos

Produto significa o resultado que obtemos após a multiplicação.

Em álgebra xy significa x multiplicado por y

E (a+b)(a−b) significa (a+b) multiplicado por (a−b) . Usamos muito isso aqui!

Produtos Binomiais Especiais

Então, quando multiplicamos binômios, obtemos... Produtos binomiais!

E veremos três casos especiais de multiplicação de binômios... então eles são Produtos Binomiais Especiais .

1. Quadrado da soma

O que acontece quando elevamos um binômio ao quadrado (ou seja, multiplicamos por ele mesmo) .. ?

(a+b) ² = (a+b)(a+b) = ... ?

O resultado:

(a+b) ² = a ² + 2ab + b ²

Esta ilustração mostra por que funciona:

 

2. Quadrado da diferença

E o que acontece quando elevamos ao quadrado um binômio com um menos dentro?

(a−b) ² = (a−b)(a−b) = ... ?

O resultado:

(a−b) ² = a ² − 2ab + b ²

Se você quiser ver o porquê, veja como o quadrado (a−b) ² é igual ao quadrado grande a ² menos os outros retângulos:

(a−b) ² = a ² − 2b(a−b) − b ²
= a ² − 2ab + 2b ² − b ² 
= a ² − 2ab + b ²

3. Produto da soma pela diferença

E então há mais um caso especial... que tal (a+b) vezes (a−b) ?

(a+b)(a−b) = ... ?

O resultado:

(a+b)(a−b) = a² − b²

E é chamada de " diferença de dois quadrados " (os dois quadrados são a ² e b ² ).

Esta ilustração mostra por que funciona:

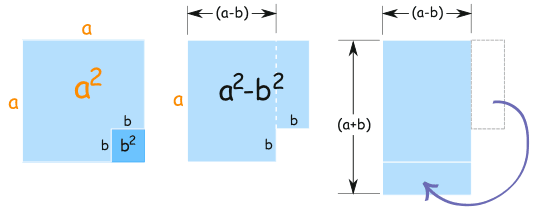a 2 − b 2      é igual a       (a+b)(a−b)

Nota: (a−b) pode ser o primeiro e (a+b) o segundo:

(a−b)(a+b) = a ² − b ²

Os Três Casos

Aqui estão os três resultados que acabamos de obter:

(a+b) 2	= a2 + 2ab + b2	}	os "trinômios quadrados perfeitos"
(a-b) 2	= a 2 − 2ab + b 2
(a+b)(a−b)	= a 2 − b 2		a "diferença de quadrados"

Lembre-se desses padrões, eles economizarão seu tempo e o ajudarão a resolver muitos quebra-cabeças de álgebra.

Usando-os

Até agora, usamos apenas "a" e "b", mas eles podem ser qualquer coisa.

Exemplo: (y+1) ²

Podemos usar o caso (a+b) ² em que "a" é y e "b" é 1:

(y+1) ² = (y) ² + 2(y)(1) + (1) ² = y ² + 2y + 1

Exemplo: (3x−4) ²

Podemos usar o caso (ab) ² em que "a" é 3x e "b" é 4:

(3x−4) ² = (3x) ² − 2(3x)(4) + (4) ² = 9x ² − 24x + 16

Exemplo: (4a+2)(4a−2)

Sabemos que o resultado é a diferença de dois quadrados, porque:

(a+b)(a−b) = a ² − b ²

então:

(4a+2)(4a−2) = (4a) ² − (2) ² = 16a ² − 4

Às vezes, podemos ver o padrão da resposta:

Exemplo: quais binômios se multiplicam para obter 4x ² − 9

Hmmm... isso é a diferença de dois quadrados?

Sim!

4x ² é (2x) ² , e 9 é (3) ² , então temos:

4x ² − 9 = (2x) ² − (3) ²

E isso pode ser produzido pela fórmula da diferença de quadrados:

(a+b)(a−b) = a ² − b ²

Assim ("a" é 2x e "b" é 3):

(2x+3)(2x−3) = (2x) ² − (3) ² = 4x ² − 9

Portanto, a resposta é que podemos multiplicar (2x+3) e (2x−3) para obter 4x ² − 9