Fatoração em álgebra
Fatores
Os números tem fatores:
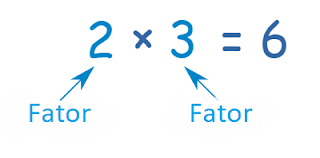
E expressões (como x2 +4x+3 ) também possuem fatores:
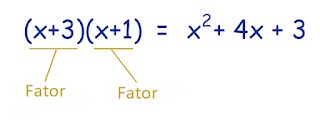
Fatoração
Fatoração: Encontrar o que multiplicar para obter uma expressão.
É como "dividir" uma expressão em uma multiplicação de expressões mais simples.
Exemplo: fator 2y+6
Ambos 2y e 6 têm um fator comum de 2:
Assim, podemos fatorar toda a expressão em:
2y+6 = 2(y+3)
Então 2y+6 foi "fatorado em" 2 multiplicado por (y+3)
Fatoração também é o oposto de Expandir:
Fator comum
No exemplo anterior vimos que 2y e 6 tinham um fator comum de 2
Mas para fazer o trabalho corretamente, precisamos do maior fator comum , incluindo quaisquer variáveis
Exemplo: fator 3y 2 +12y
Em primeiro lugar, 3 e 12 têm um fator comum de 3 .
Então poderíamos ter:
3y 2 +12y = 3(y2 +4y)
Mas nós podemos fazer melhor!
3y 2 e 12y também compartilham a variável y .
Juntos, isso faz 3 y :
- 3y 2 é 3y . y
- 12y é 3y . 4
Assim, podemos fatorar toda a expressão em:
3y2 +12y = 3y(y+4)
Verifique: 3y(y+4) = 3y × y + 3y × 4 = 3y2 +12y
Fatoração mais elaborada
Os exemplos foram simples até agora, mas a fatoração pode ser mais elaborada.
Porque temos que descobrir o que foi multiplicado para produzir a expressão que nos foi dada!
É como tentar descobrir quais ingredientes
entraram em um bolo para torná-lo tão delicioso.
Experiência ajuda
Com mais experiência, a fatoração torna-se mais fácil.
Exemplo: Fator 4x 2 − 9
Hmmm... não parece haver nenhum fator comum.
Mas conhecendo o Produtos Binomiais Especiais nos dá uma pista chamada "diferença de quadrados" :

Como 4x 2 é (2x) 2 , e 9 é (3) 2 ,
Então nós temos:
4x 2 − 9 = (2x) 2 − (3) 2
E isso pode ser produzido pela fórmula da diferença de quadrados:
(a+b)(a−b) = a 2 − b 2
Onde a é 2x e b é 3.
Então vamos tentar fazer isso:
(2x+3)(2x−3) = (2x) 2 − (3) 2 = 4x 2 − 9
Sim!
Portanto, os fatores de 4x 2 − 9 são (2x+3) e (2x−3) :
Resposta: 4x 2 − 9 = (2x+3)(2x−3)
Como você pode aprender a fazer isso? Fazendo muita prática e conhecendo "Identidades"!
Lembre-se dessas identidades
Aqui está uma lista de "Identidades" comuns (incluindo a "diferença de quadrados" usada acima).
Vale a pena lembrá-los, pois podem facilitar a fatoração.
|
| a 2 − b 2 | = | (a+b)(a−b) |
| a2 + 2ab + b2 | = | (a+b) (a+b) |
| a 2 − 2ab + b 2 | = | (a-b) (a-b) |
| a3 + b3 _ | = | (a+b)(a 2 −ab+b 2 ) |
| a 3 − b 3 | = | (a−b)(a 2 +ab+b 2 ) |
| a 3 +3a 2 b+3ab 2 +b 3 | = | (a+b) 3 |
| a 3 −3a 2 b+3ab 2 −b 3 | = | (a-b) 3 |
Existem muitos mais como esses, mas esses são os mais úteis.
Dica
A forma fatorada é geralmente a melhor.
Ao tentar fatorar, siga estas etapas:
- "Fatore" quaisquer termos comuns
- Veja se ele se encaixa em alguma das identidades, além de mais alguma que você conheça
- Continue até que você não possa fatorar mais
Mais exemplos
A experiência ajuda, então aqui estão mais exemplos para ajudá-lo no caminho:
Exemplo: w 4 − 16
Um expoente de 4? Talvez possamos tentar um expoente de 2:
w 4 − 16 = (w 2 ) 2 − 4 2
Sim, é a diferença de quadrados
w 4 − 16 = (w 2 + 4)(w 2 − 4)
E "(w 2 − 4)" é outra diferença de quadrados
w 4 − 16 = (w 2 + 4)(w+ 2)(w− 2)
Isso é o mais longe que posso ir (a menos que eu use números imaginários)
Exemplo: 3u 4 − 24uv 3
Remova o fator comum "3u":
3u 4 − 24uv 3 = 3u(u 3 − 8v 3 )
Então uma diferença de cubos:
3u 4 − 24uv 3 = 3u(u 3 − (2v) 3 )
= 3u(u−2v)(u 2 +2uv+4v 2 )
Isso é o mais longe que posso ir.
Exemplo: z 3 − z 2 − 9z + 9
Tente fatorar os dois primeiros e os dois segundos separadamente:
z 2 (z−1) − 9(z−1)
Uau, (z-1) está em ambos, então vamos usar isso:
(z 2 −9)(z −1)
E z 2 −9 é uma diferença de quadrados
(z−3)(z+3)(z−1)
Isso é o mais longe que posso ir.
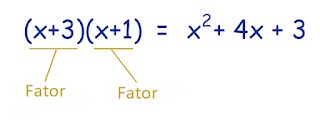



Nenhum comentário:
Postar um comentário