Expoentes

Expoentes

O expoente de um número diz quantas vezes usar o número em uma multiplicação.

 

Em 8 ² o "2" diz para usar 8 duas vezes em uma multiplicação,

então 8 ² = 8 × 8 = 64

Em palavras: 8 ² poderia ser chamado de "8 elevado a 2" ou "8 elevado a segunda potência", ou simplesmente "8 elevado ao quadrado"

Mais alguns exemplos:

Exemplo: 5 ³ = 5 × 5 × 5 = 125

• Em palavras: 5³ poderia ser chamado de "5 elevado à terceira potência", "5 elevado a 3" ou simplesmente "5 ao cubo"

Exemplo: 2 ⁴ = 2 × 2 × 2 × 2 = 16

• Em palavras: 2⁴ poderia ser chamado de "2 elevado a 4" ou "2 elevado a quarta potência"

Os expoentes facilitam a escrita e o uso de muitas multiplicações

Exemplo: 9 ⁶ é mais fácil de escrever e ler do que 9 × 9 × 9 × 9 × 9 × 9

Observação: os expoentes também são chamados de potências ou índices.

Você pode multiplicar qualquer número por ele mesmo

quantas vezes quiser usando expoentes.

Então generalizando :

a n diz para você multiplicar a por si mesmo n vezes ou infinita vezes: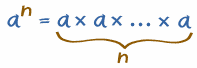

Outra forma de escrever

Às vezes, as pessoas usam o símbolo ^ (acima da base), pois é fácil de digitar.

Exemplo: 2^4 é o mesmo que 2 ⁴

• 2^4 = 2 × 2 × 2 × 2 = 16

Expoentes Negativos

Como todo número inteiro pode ser transformado em uma fração com denominador 1, podemos inverter a fração e mudar o sinal do expoente.

Exemplo: 8 ^-1 = 18 ¹ = 0,125 

Podemos continuar assim:

Exemplo: 5 ^-3 =15×15×15= 0,008

Mas muitas vezes é mais fácil fazer assim:

5 ^-3 também pode ser calculado como:

15 × 5 × 5

=

15 ³

 =

1125

 = 0,008

Negativo? Vire o positivo!

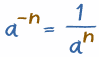Esse último exemplo mostrou uma maneira mais fácil de lidar com expoentes negativos: Calcule o expoente positivo ( a n ) Em seguida, pegue o equivalente (ou seja, 1/a n )

Mais exemplos:

Expoente Negativo		Equivalente com Expoente Positivo		Resultado
4 -2	=	1 / 4 2	=	1/16 = 0,0625
10 -3	=	1/10 3	=	1/1.000 = 0,001
(-2) -3	=	1 / (-2) 3	=	1/(-8) = -0,125

E se o expoente for 1 ou 0?

1		Se o expoente for 1, você terá apenas o próprio número (exemplo 9 1 = 9 )
0		Se o expoente for 0, você obtém 1 (exemplo 9 0 = 1 )
		Mas e quanto a 0 0 ? Pode ser 1 ou 0, então dizemos que é "indeterminado" .

Tudo faz sentido

Se você olhar para essa tabela, verá que os expoentes positivos, zero ou negativos são realmente parte do mesmo padrão (bastante simples):

Exemplo: potências de 5
	.. etc..
5 2	5 × 5	25
5 1	5	5
5 0	1	1
5 -1	15	0,2
5 -2	15×15	0,04
	.. etc..

Tenha cuidado ao agrupar

Para evitar confusão, use parênteses () em casos como este:

Com () :	(−2) 2 = (−2) × (−2) = 4
Sem () :	−2 2 = −(2 2 ) = −(2 × 2) = −4

Com () :	(ab) 2 = ab × ab
Sem () :	ab 2 = a × (b) 2 = a × b × b